公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「平行四辺形の面積の求め方」をご覧ください。 扇形の面積を求める公式は、S = πr^2 × x/360 = 1/2 lr で表されます。扇形の面積 S × a ∘ 360 ∘ 例1) 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから、直径で計算する円周の式によって,楕円の面積公式より答えは π ⋅ 3 ⋅ 4 = 12 π \pi \cdot 3\cdot 4=12\pi π ⋅ 3⋅ 4 = 12π ここから,楕円の面積公式の3通りの証明を紹介します。 グラフの拡大を用いる方法 愚直に定積分を計算する方法 ガウスグリーンの定理を使う方法 1は積分を知ら

円とおうぎ形 応用 無料で使える中学学習プリント
扇形面積求め方 高校
扇形面積求め方 高校-それぞれの図形の見方、考え方について学んでいきましょう! おうぎ形の公式って何だっけ? という方は、まずこちらの記事で復習しておいてね! ⇒ おうぎ形面積、弧の長さ、中心角の求め方を問Jw_cad その他の〔 測定 〕コマンドの「面積測定」を行うとき、図形に丸面取り処理などが施されている図形の面積を測定するときに使うのが「(弧 指定」ボタンです。 円弧を含む面積測定の使い方 「 測定 」コマンドを実行し、コントロールバーの「面積測定」ボタンを 左クリック します。




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
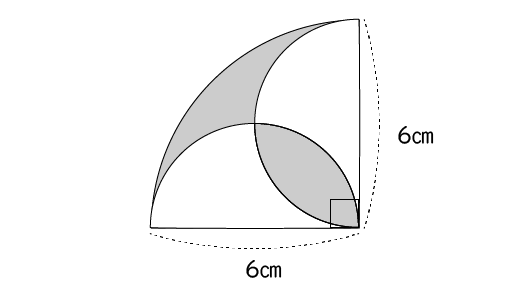
デジタル教材 『扇形の面積』 1618 熊本市教育センター ICT 支援室 扇形の面積の求め方を視覚的にわかりやすく説明する教材です。 教材は以下の3つで構成されています。 「01_円の面積exe」 円の面積の説明をアニメーションで行います。 「02_半円の面積 側面である扇形の面積を求めようとすると、扇形の公式から分かるように 中心角が必要になります。 というわけで、 まずは扇形の中心角を求めていきます。 底面の円周の長さと側面の弧の長さが等しいことを利用すると 単元:複雑な面積の求め方 講師 下の図の影になっている部分の面積を求めてください。 生徒 扇形の半分の図形からうまく残りの白部分を引いた式ができれば解けそうですね。 講師 Goodです。 さてどのように引いたらよいでしょうか。 ヒントは、図
弓形・扇形面積の計算式 ①扇形の面積(Fun) 扇OCD の面積(F)は θ θ 2π 2= 2 r2・・・・F ②弓形の面積(Bow) 三角形OCD の面積(S)は 2×三角形OCB OB×BC 2 θ θ Cos( 2 )×sin( 2 ) =2× 2 θ θ =Cos( 2 )×sin( 2 )・・・・S したがって弓形OCD の面積(B)はF 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいの円錐の側面積の求め方が分かりません。 そのため、以下の公式になります。 クリックして Bing でレビューする1011 円すいの側面積の求め方 — Duration 747 ですが、これを活用しない限りは現状は変わらないです。 14
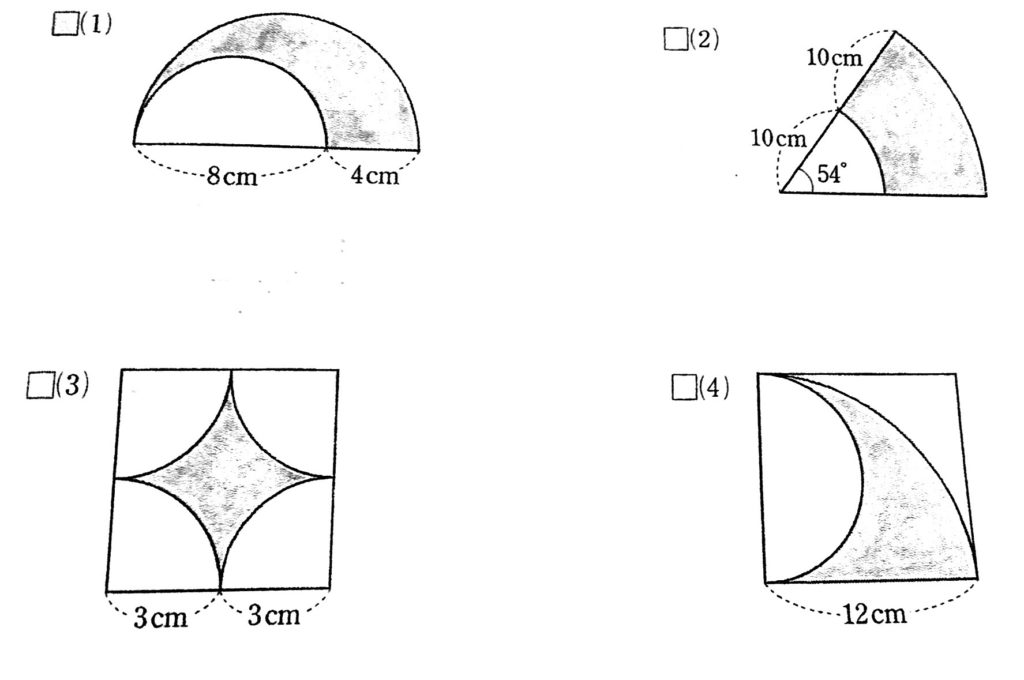
円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l それぞれについて詳しく見ていきおうぎ形の弧の長さと面積の求め方|小学生に教えるための解説 管理人 10月 5, 18 / 11月 26, 18 おうぎ形は『円』と『比』の単元が関係するため、両方をしっかり抑えていないと理解することができないでしょう。 円とおうぎ形のいろいろな面積の問題です。 学習のポイント 正方形とおうぎ形を合わせた形の面積を素早く求められるようにしましょう。 *色のついた部分の面積を求めます。 4分の1のおうぎ形2つから正方形をひく、4分の1のおう




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
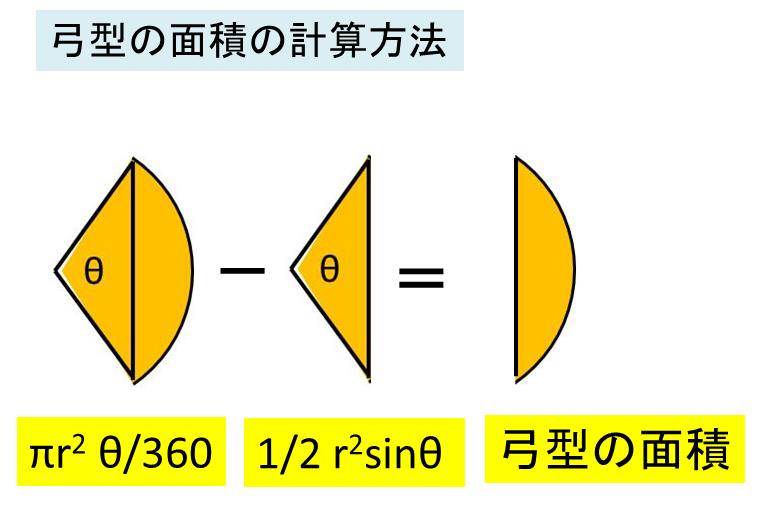
弓形の面積 弓形とは円とその割線 (円と異なる二点で交わる直線)で囲まれる図形で、図1における網掛け部分のような図形です。 実はその反対側も弓形です。 以下では弓形の面積をS、円の半径をr、弓形の基になる扇形の中心角をθとします。 但し、中心★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料 弧の長さ と 元の円の円周を 比較する このおうぎ形の元になった、 半径 3cm の円 を考えます 半径 3cm の円の 円周の長さ は $\textcolor{red}{直径(半径\times2)\times314}$ より $3\times2\times314=14 cm$ おうぎ型の弧の長さ(問題文より$314cm$)を比べると




三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




円 扇形 の面積 周や弧の長さの公式 数学fun
扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 ここでは、おうぎ形と正方形が組み合わさった面積を求める問題を見ていきます。 おうぎ形と正方形の面積その1 例題1 次の図は、正方形とおうぎ形を組み合わせた図形です。色のついた部分の面積を求めなさい。 このような部分の面積ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積
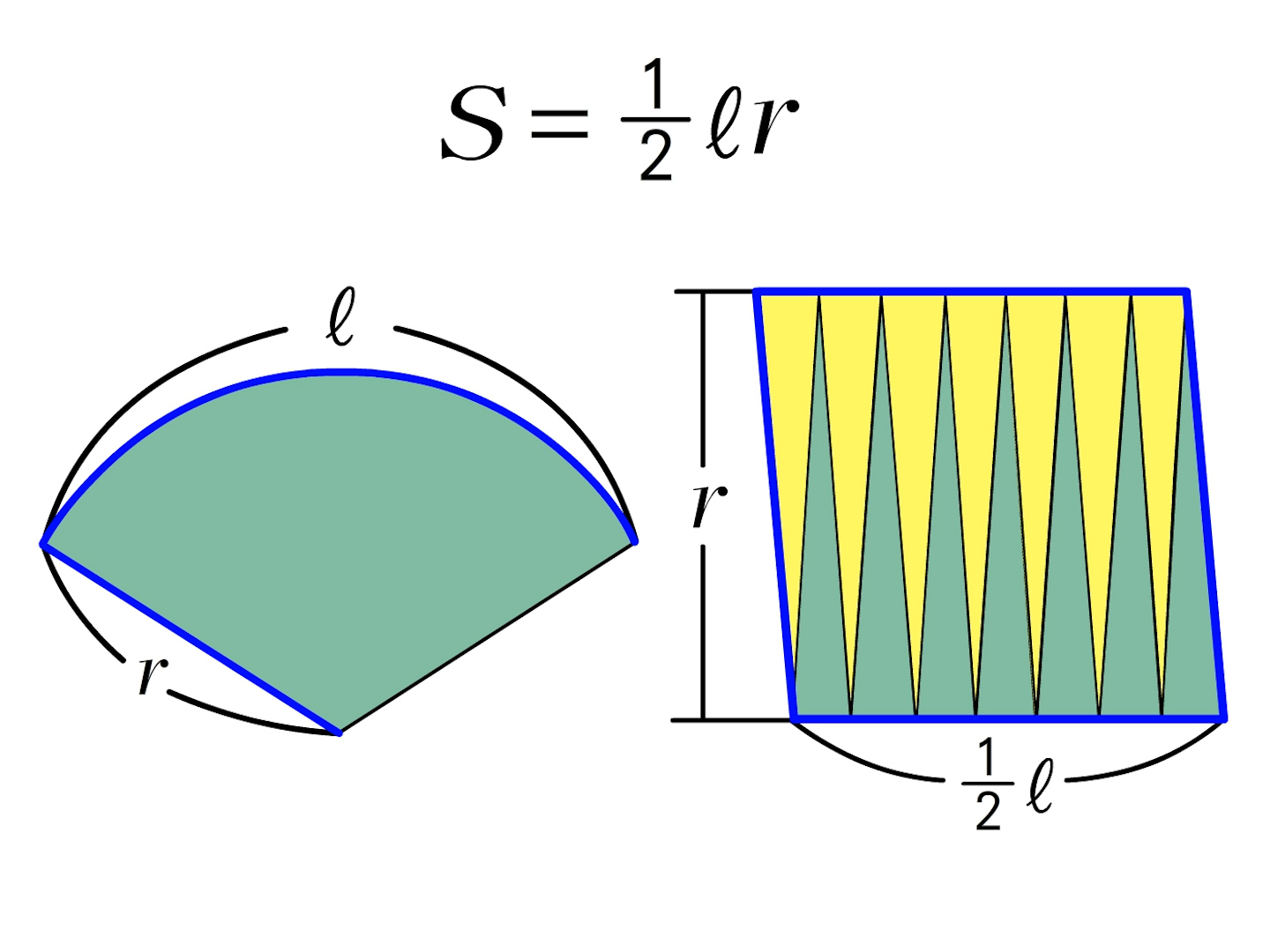



1年 おうぎ形の面積 数学イメージ動画集 大日本図書
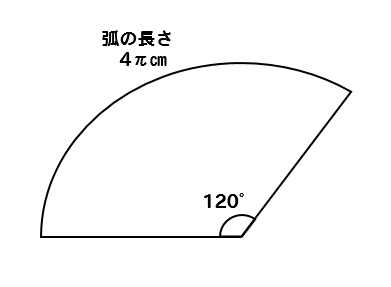



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
一般角と弧度法、扇形の弧長l=rθと面積S=1/2r²θ スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 三角比から三角関数へ}} \\ 5zh 数Iでは,\ 三角比$\sin\theta,\ \cos\theta,\ \tan\theta$について学習した \\ 2zh 三角形の計量を目的としていたので《円・半円・弧・扇形》の円周・面積の求め方と公式一覧 算数 中学受験 《円・半円・弧・扇形》の円周・面積の求め方と公式一覧 小学校5年生~6年生で学習する『円』に関する公式をまとめて一覧にしました。A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau
扇形の面積の求め方で側面積を出す → 母線(もとの円の半径)×母線×円周率(π:314)×中心角の大きさ÷360=側面積 ←4 最後に底面積と側面積を足し合わせれば四角錐の表面積が求められます。 扇形の面積を求めるときに困惑する人が多いかもしれません。 =半径×半径×円周率× 中 心 角 360 ° ※扇形の面積は、円の面積に 中 心 角 360 ° をかけることで求めることが出来ます。 ※円周率は、小学校ではふつう314を使います。円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題 錐体の表面積6 宿題解説 正四角錐の体積 表面積の求め方 Youtube 円錐は1 3 中学生に分かるように真剣に考えてみ 円錐の表面積の求め方は完全パターン化できる!




円とおうぎ形 応用 無料で使える中学学習プリント



3
・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を 僕は円錐の表面積の求め方は、まず 扇形の弧の長さ=底面の円周なので、 360分のaの「a」を求めます。 aは 扇形の弧の長さが底面の円周と同じ 数字にする為の数字なので、aの計算を 間違えると計算ミスします。
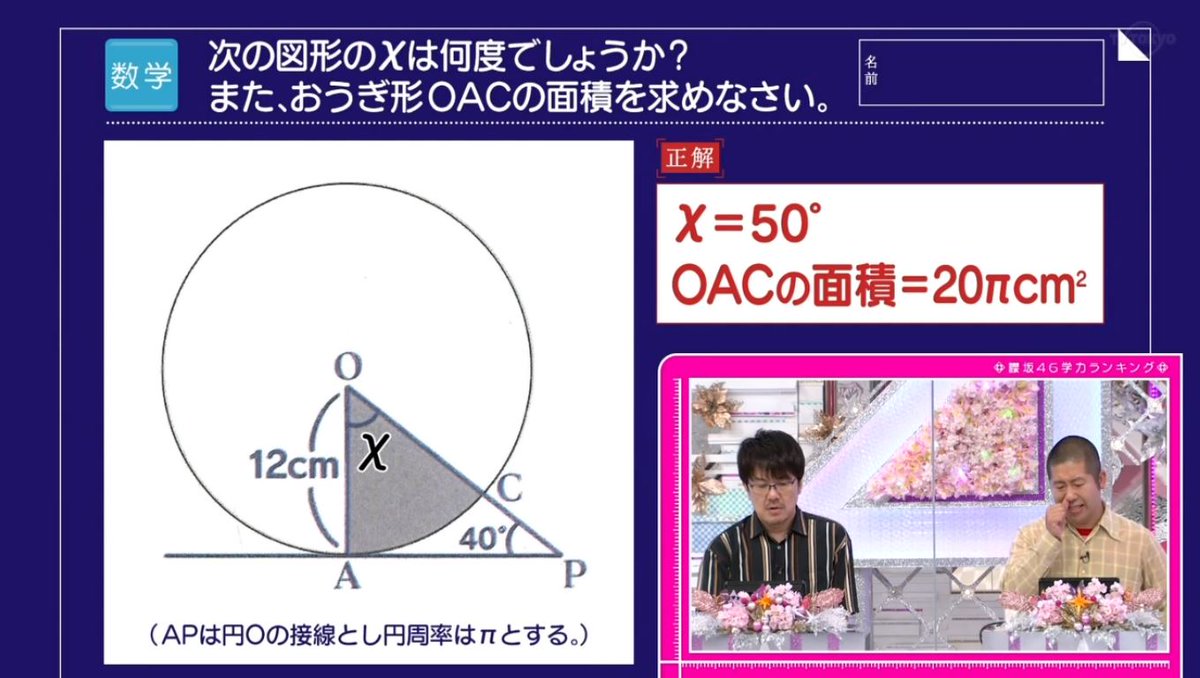



チョラッペ 角度分かるけど 扇形の面積の求め方なんて完全に忘れてたw 三角形180 90 40 X 50 扇形面積 半径 半径 P 中心角度 360 代入すると 12 12 P 50 360 p なのでp ってことですね そこ曲がったら櫻坂 T Co Erkwnrjtob
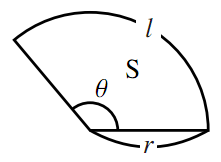



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。初等幾何学における弓形(ゆみがた、英 circular segment (記号 ⌓ )は、円板から割線または弦によって残りの部分から「切り取られる」部分を言う。 より厳密には、円の劣弧(中心角が180°未満の弧)とその円弧の両端点を結ぶ弦で囲まれた二次元の領域を弓形という。1 直径8の円の上半分の面積 直径が8だから半径は4.半円だから円の面積の半分:4 2π ÷2=8 π π 採点する やり直す 解説 2 半径 6 ,中心角が1°の扇形の面積 1°だから円(360°)の3分




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
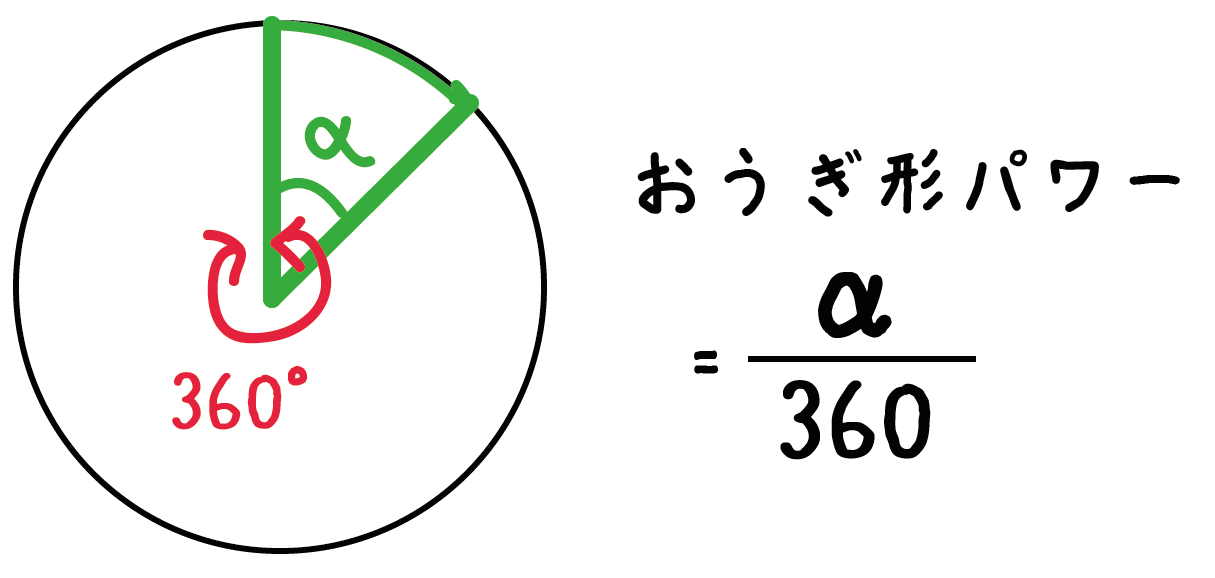



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




ボード 復習 のピン




扇形の半径の求め方 計算のやり方をイチから解説していくぞ 中学数学 理科の学習まとめサイト



欠けた円 欠円 や弓形の面積の計算方法




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




標準 おうぎ形と正方形の面積 なかけんの数学ノート




圓的周長與面積 19 扇形的面積計算 Youtube




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
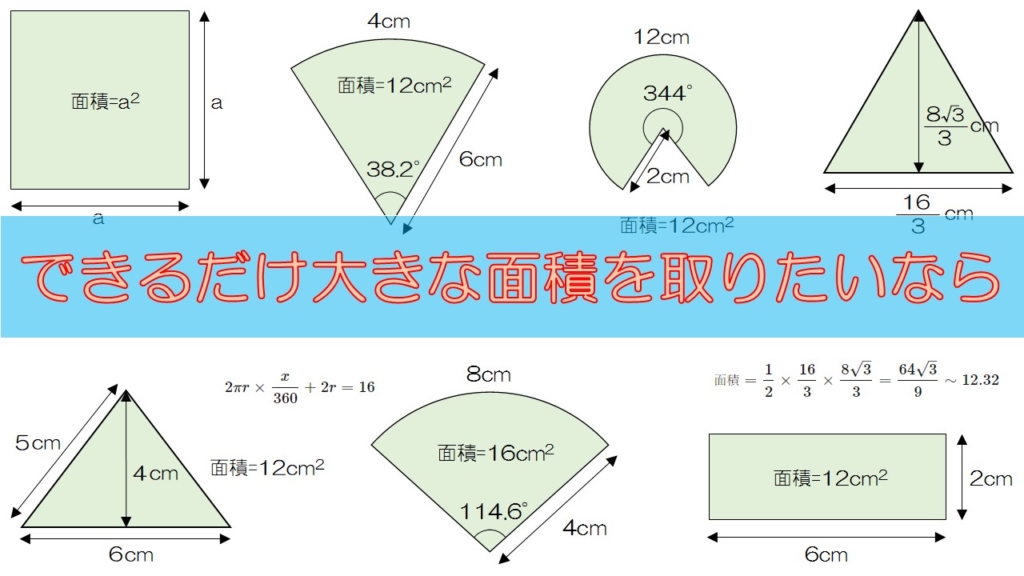



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




扇形 の 面積 の 求め 方 小学生 かわいいドラえもん




扇形の弧の長さの求め方 公式と計算例



この扇形の図形の面積の求め方をご教示ください 扇型の中の円の半径 Yahoo 知恵袋



おう ぎ 形 の 面積 求め 方
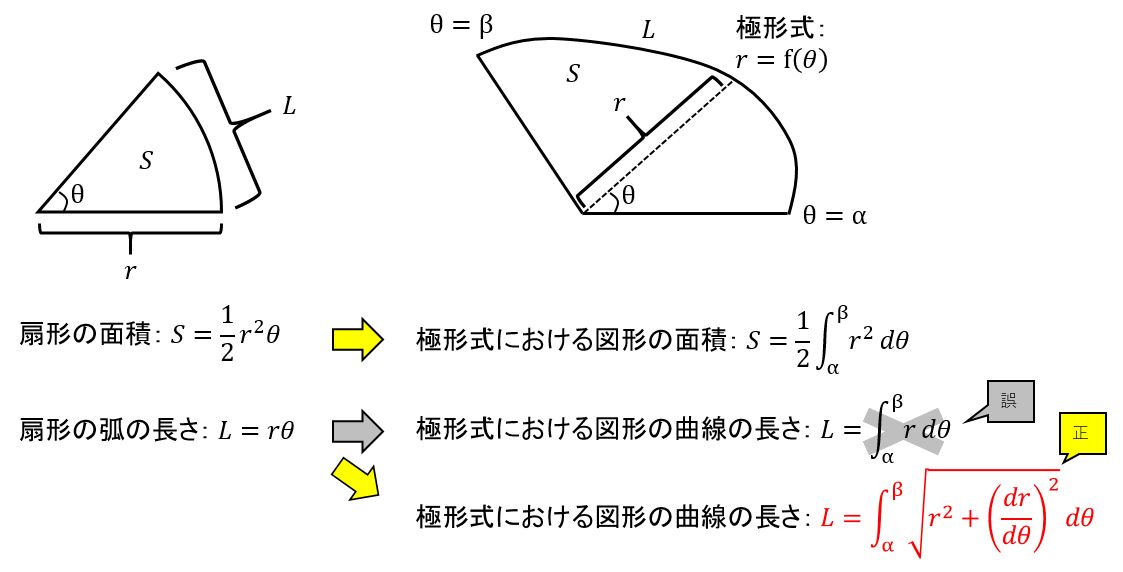



ラブリー扇形 弧の長さ 公式 最高のカラーリングのアイデア
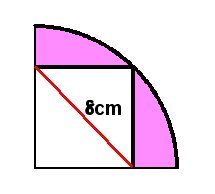



扇形と正方形



扇形の面積と公式 面積計算機
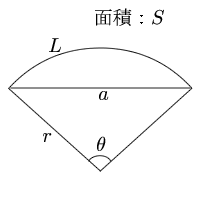



扇形 面積の計算 計算サイト




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook
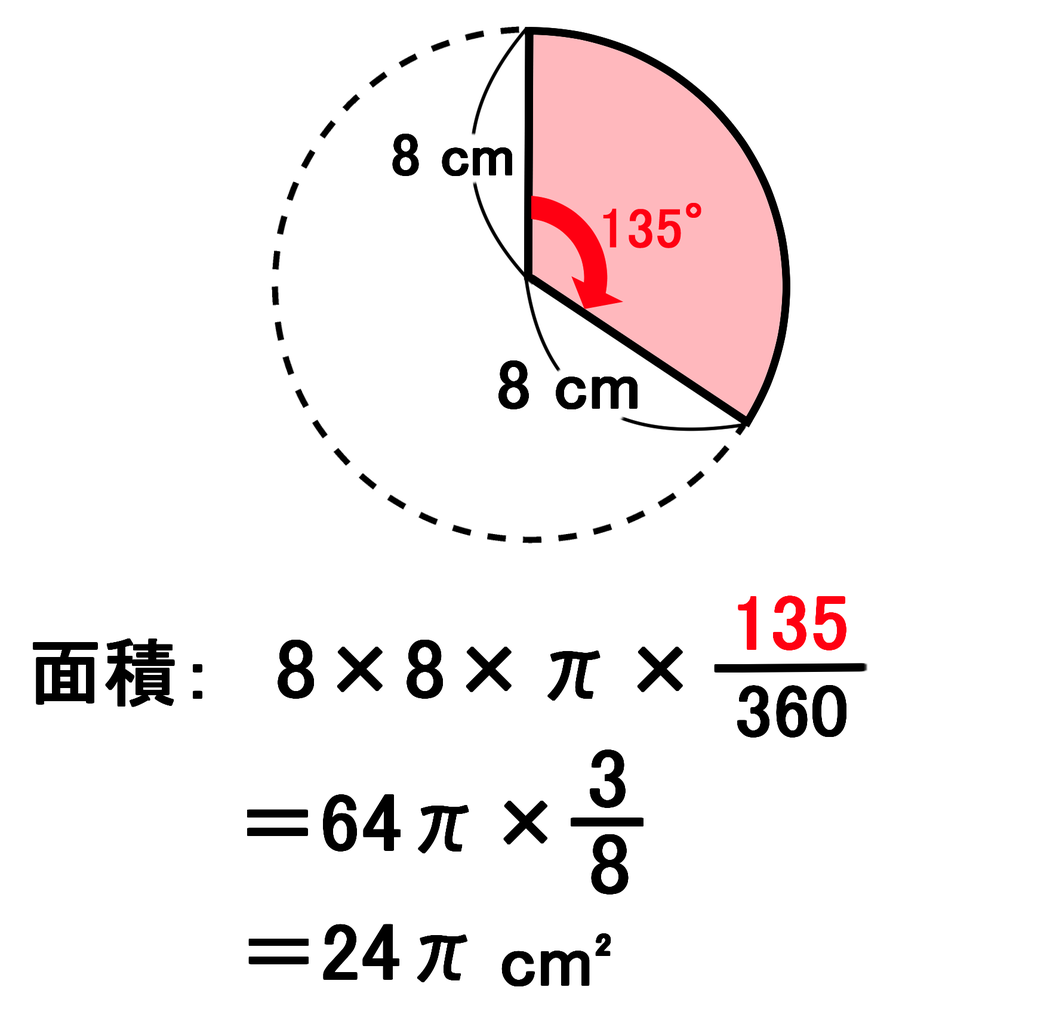



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという問題です Clear
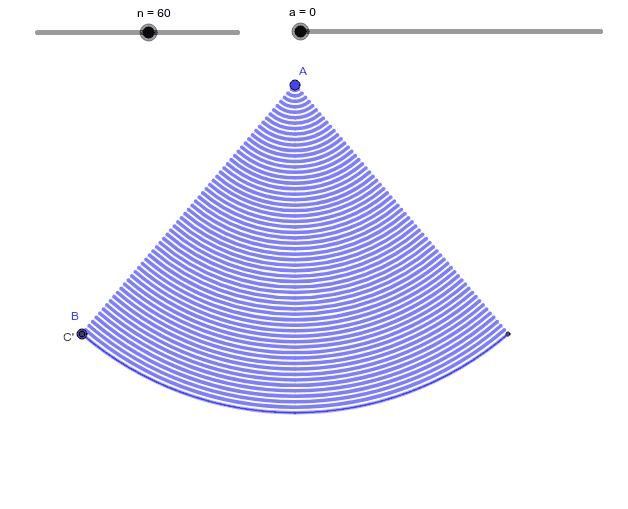



扇形の面積 Geogebra




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




公式を図解 すい体の体積 円すいの表面積の求め方



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




おうぎ形の面積 弧の長さ 数学ノート




新着扇形 面積 の 求め 方 最高のカラーリングのアイデア




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe




扇形の面積の求め方 公式と計算例




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
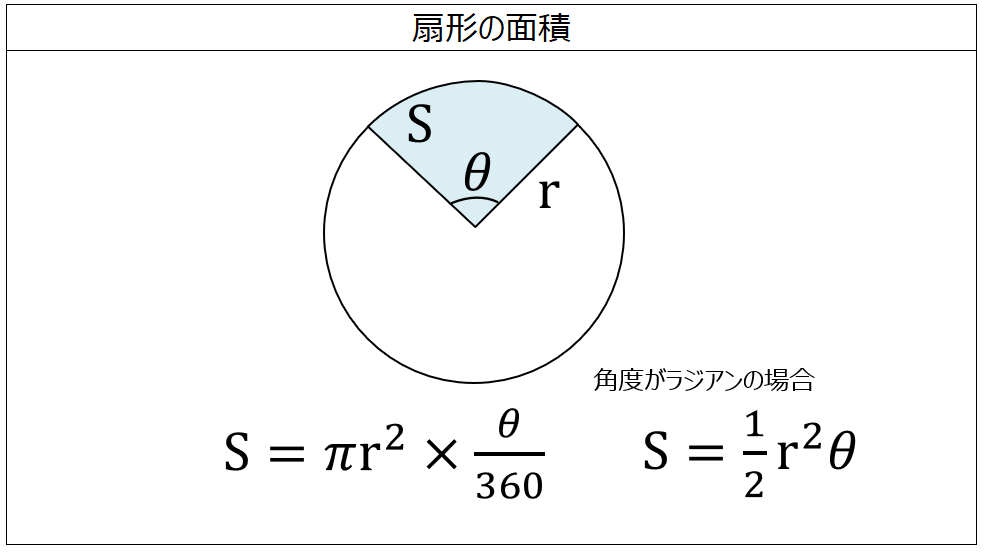



面積の計算 扇形 製品設計知識
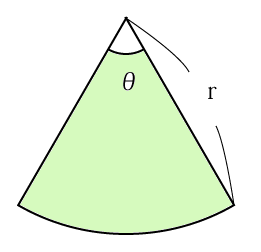



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




円錐の表面積の求め方 You Look Too Cool




弓形の面積 香料ゐっすゐの夢




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




色のついた部分の面積の求め方を教えてください Clear
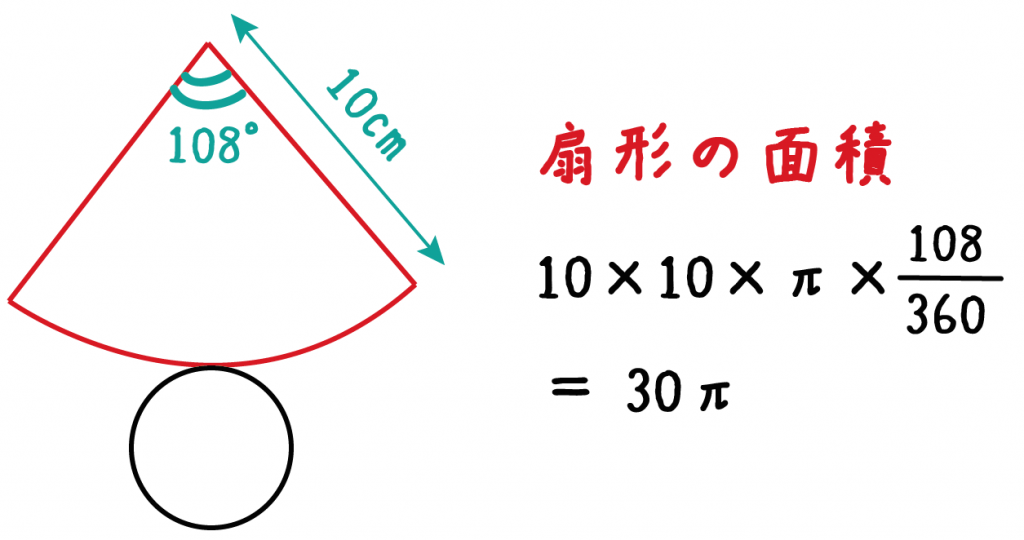



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
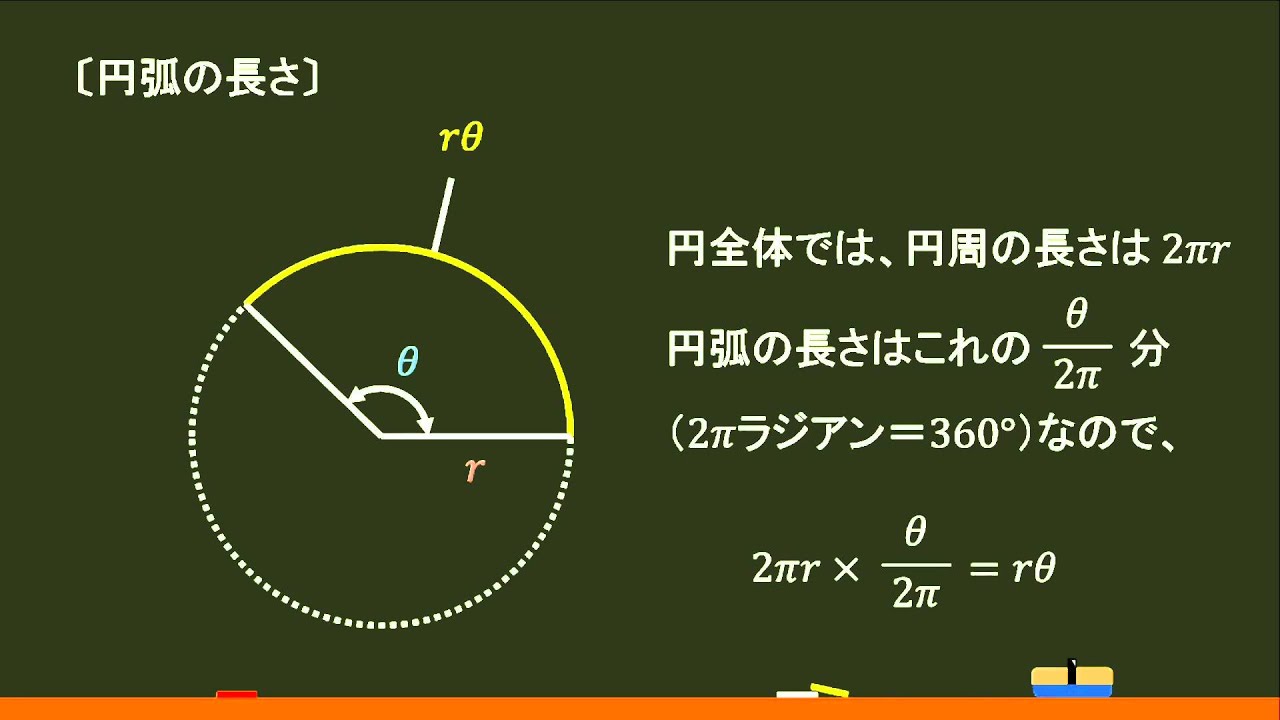



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube
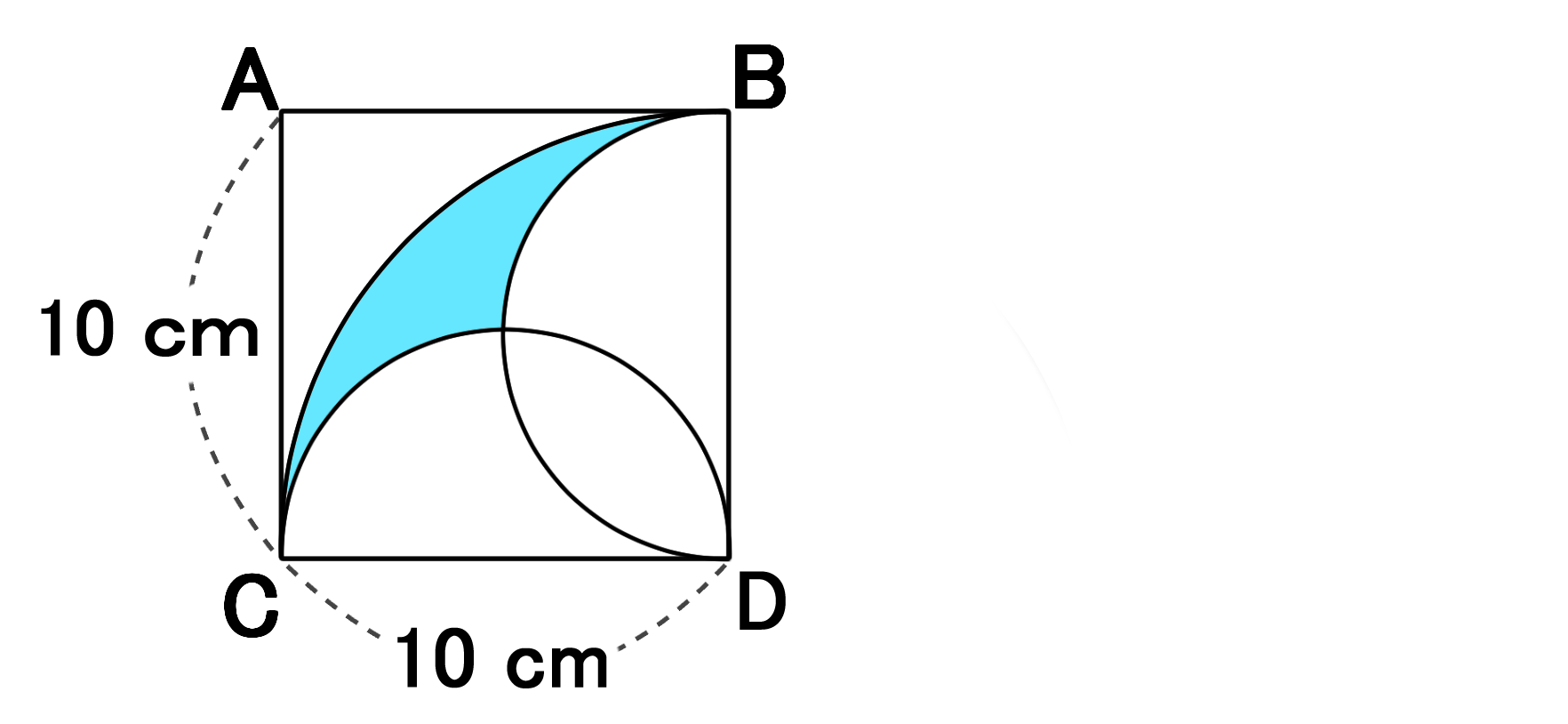



バカでもわかる 中学数学




極方程式の面積 扇形積分 おいしい数学




円弧面積の計算式



50 扇 面積 求め方




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー
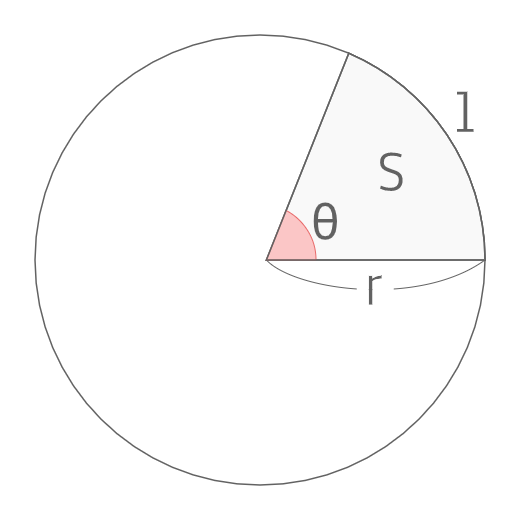



高校数学 扇形の弧の長さと面積 の公式とその証明 Enggy




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube
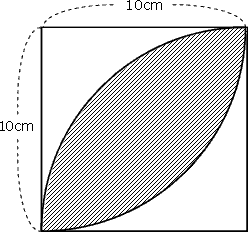



面積の求め方 算数の教え上手 学びの場 Com



扇形の面積の求め方1 2 弧長 半径という公式が理解できません Yahoo 知恵袋




扇形面積公式弧長14 Zilhc




覚えなくていい 円の面積 東大生の高校数学ブログ
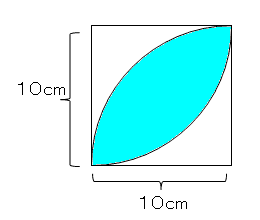



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
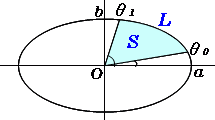



楕円扇形の面積 高精度計算サイト




扇形の弧の長さと面積 計算ドリル 問題集 数学fun



扇形の面積は 1分でわかる意味 公式 求め方 ラジアンとの関係




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




正方形扇形面積 扇 おうぎ 形の面積を求める公式と弧の長さの求め方翻譯此網頁 Voajcr




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月
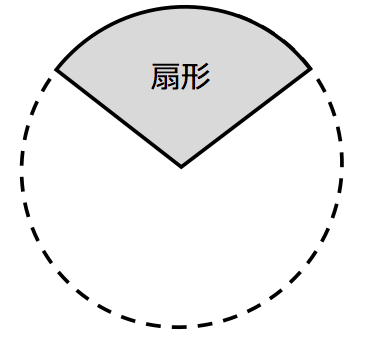



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
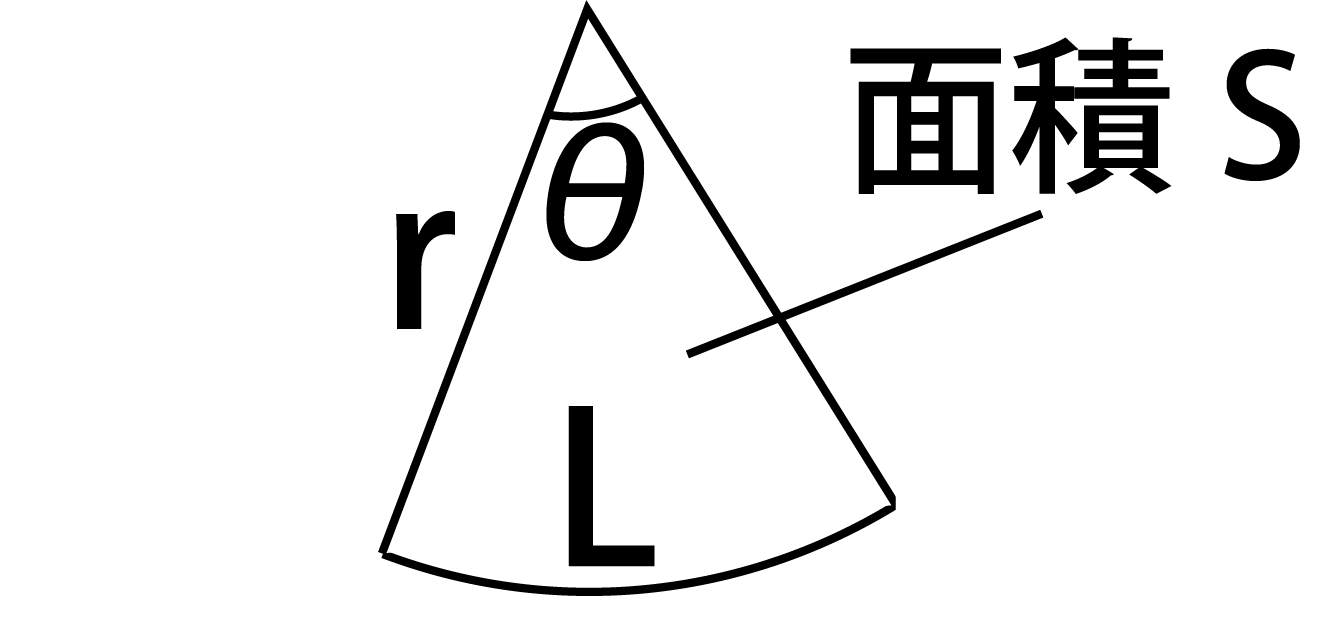



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



1



円と扇形 中学受験ー算数解き方ポータル




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
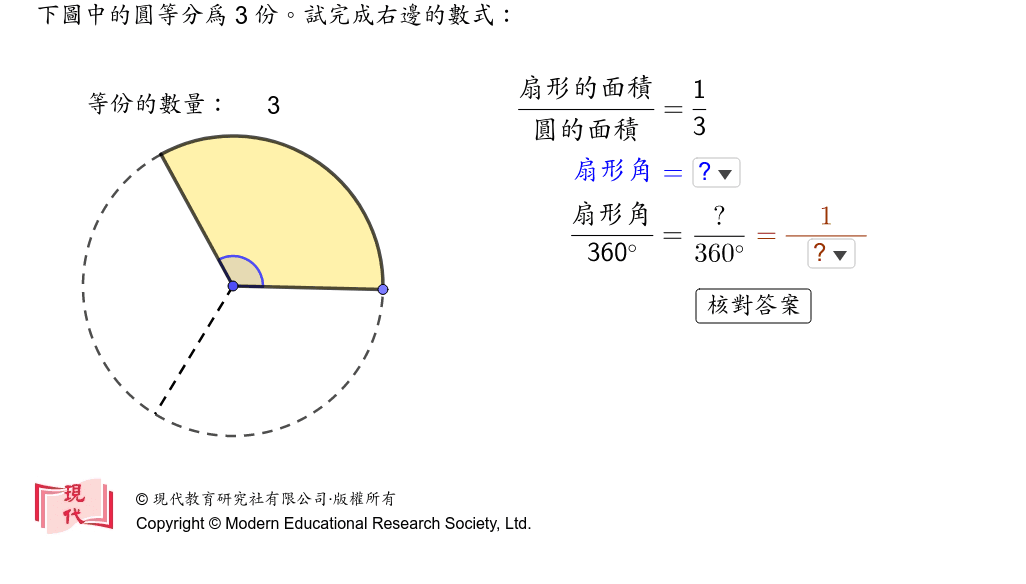



扇形面積公式 Geogebra



Spi M54e217p7lcis9d Com Category E5 9b E5 81 Ae E9 9d E7 8d




極方程式の面積 扇形積分 おいしい数学




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




面積の求め方 算数の教え上手 学びの場 Com
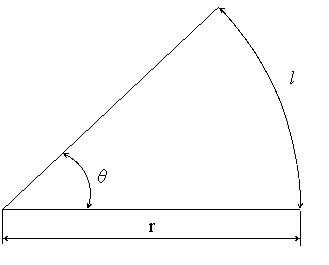



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ




扇形の面積の求め方を教えてください Clear



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



中心角が分からない扇形の面積の求め方の裏ワザ 爽のつぼやき




扇形の面積の求め方 公式と計算例



0 件のコメント:
コメントを投稿