故 x=3, y=2 為二元聯立方程組的解。 三、解應用問題 : 利用二元一次聯立方程式解決生活情境中的問題,解題步驟為: 1 認清題意設定兩個適當的未知數。 2 依題意列出二元一次聯立方程式。 3 利用代入消去法或加減消去法解二元一次聯立方程式。一元一次方程式 以前我們有使用( )或是 代表未知數的值,如: 雨婷原本有一些糖果,她吃掉了 顆,還剩下 顆。 雨婷原本有幾顆糖果? 設雨婷有( )顆糖果,根據題意可以列出式子( ) = ,可以知道( ) = = ,所以雨婷原本有 顆糖果。;二元一次聯立方程式 應用問題 B 12 最近全球科學家探討溫室效應, 一致認為造成地球溫室效應之罪魁禍首在於二氧化碳的排放 。 依題意列出二元一次方程式為 500 x+ 0 y= 2400 。
代入法解二元一次方程组练习题 松鼠文库
二元一次方程式 グラフ 問題
二元一次方程式 グラフ 問題-二元一次聯立方程式解的幾何意義 根據上面的介紹,知道可以把二元一次方程式畫在坐標平面上為一直線 那聯立方程式的話,就可以在坐標平面上畫出兩條線 又知道線所代表的意思是方程式的解 而二元一次方程式的解為滿足兩個方程式的解翻轉學習影片描述:講師何佳穎 講師簡介 我叫何佳穎,畢業於政治大學,個性積極開朗,從小對於數學有濃厚的興趣,希望能把數學的美傳遞給大家,另外,也對橄欖球相當喜愛,歡迎有興趣的同學來討論。 影片簡介 本影片介紹何謂聯立方程式、如何列式、怎樣算是聯立方程式的解




二元一次聯立方程式的應用題3 Youtube
影片:例題二元一次方程式:應用問題 1,數學 > 國中 > 七年級 > 均一版 > 二元一次聯立方程式 > 二元一次方程式應用問題。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己的未來。第二冊 主題二 直角坐標平面與二元一次方程式的圖形 22 二元一次方程式的圖形 Part1:主題探索窗 探索一 二元一次方程式 (解) 的圖形之意義 範例 1 已知 x=0 、 y=1 為方程式 y=x1 的一組解,我們用 (0,1) 來表示此組解,並可將它畫在直角坐標上成為一個點2 解二元一次方程式 ,將 2+ 7後得到下列哪一個式子?(A) 47x= (B) 37x= 47x=21 (D) 47y= 2 志斌在完成數學習作中的算式求值問題後,不小心將甲、乙、丙、丁的資料塗 汙了,如表所示,則下列選項何者正確? 甲 -2 乙 1 2x-3y 19 丙
AⅣ4 理解二元一次聯立方程式及其解的意義,並能以代入消去法與加減消去法求解和驗算,以及能運用到日常生活的情境解決問題。 議 題: 閱讀素養教育 核心素養: A3 規劃執行與創新應變 更新時423 二元一次方程式的應用問題 5 直角坐標與二元一次方程式的圖形 51 直角坐標平面 511 數對與坐標 512 坐標與象限 52 二元一次方程式的圖形 資料夾名稱 二元一次聯立方程式 (ch1) 發表人 顧震宇 單位 台灣數位學苑 (k12 數學) 建立 最近修訂 5709
研究者期盼能澄清學生學習「二元一次方程式圖形」單元相關的迷思概念, 增加學生學習數學的自信心,因此,依其研究目的與待答問題配合相關文獻的搜 集彙整,而獲得了以下的研究結果: 一、依據學生作答情形所發生的迷思概念與相關文獻探討不謀而合。一元一次方程式的應用問題解題步驟 假設未知數。 依題意列出一元一次方程式。 解一元一次方程式。 驗算、檢查解是否合乎情境。 寫答,若沒有符合情境則回答「無解」。 價錢問題 簡易價格問題甲乙兩人跑步,甲每分鐘跑 x 公尺,乙每分鐘跑 y 公尺。若甲在 5 分鐘內比乙多跑 0 公尺,請依題意列出二元一次方程式。 甲、乙比賽跑步,甲的速度是乙的 15 倍。




我想請問為何二元一次不等式ax By的係數a要大於零 如果題目是給負數我自己要把他變 Clear



Http Www Topmath Org Jtest Ex 0602 Pdf
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators檢驗二元一次方程式在坐標平面上的圖形是一直線 在下圖的坐標平面上,找出方程式 x-y=0 的兩組解(-7 , -7)和(7 , 7) 所代表的點,畫一條通過這兩點的直線,稱此直線為 L,並回答下列 問題:整理二元一次方程式為 (此步驟可略) 答2x2y;2x2y;502x2y=6。 練習8 (1)一等腰梯形的上底為8公分,腰長為x公分,下底為y公分,且其周長為60公分,請依題意列出二元一次方程式 。 (2)某冷飲店販賣飲料,珍珠奶茶一杯25元,一般紅茶一杯15元, 袁太 買了x杯珍珠




怎麼用二元一次聯立方程式解題 Clear



二元一次方程各类应用题 松鼠文库
二元一次方程式學習單 學前活動 小丸子 和小玉一起去看電影「海角七號」,小丸子用她所有錢的五分之四去買爆米花,小玉用她所有錢的三分之一買可樂,結果二人共剩下 460 元,請問小丸子原有 多少元呢?二元一次聯立方程式題目二元一次方程式數學題目精采文章二元一次方程式數學題目,二元一次聯立方程式解法,解三元一次聯立方程式,一元二次方程式應用問題網路當紅,二元一次方程式,國中數學第二冊 第一章_二元一次聯立方程式 ※13二元一次聯立方程式之應用問題 解說影片之播放目錄: 觀念 七年級二元一次聯立方程式應用問題整理(77題) 七年級應用問題一直都是學生的死穴!阿杰蒐集各家的應用問題於此。大家一起努力吧! 二元ㄧ次方程式應用問題 若有需要詳解,請洽ㄚ杰。



二元一次不等式组与简单的线性规划问题 线性规划求最值




大家來解謎 解二元一次聯立方程式 導入活動 環遊數界
数学22章連立二元一次方程式「連立方程式の利用」<準備問題①> 組 番 名前 1次の問いに答えなさい(ただし,もっとも簡単な式に表しなさい。) (1)長さ2mのひもの端から,長さ25cmのひもをχ本切り取ると,残りのひもの長さはy㎝で した。二元一次聯立方程式 變數 x, y 要同時滿足兩個二元一次方程式 若 x, y 的值同時滿足兩個方程式,稱為聯立方程式的解 2 代入消去法 a 將一個方程式中的變數 x 用 y 的關係式 (如 x = by c) 代入另外一個式子 b 得到只有變數 y 的方程式,求得 y知識・技能の習得を図る問題解答 年 組 号氏名 全国学力・学習状況調査① A問題 1 (1) 二元一次方程式2x -y =1の解は,この等式を成り立たせる文字x,y の値の組である。 この等式を成り立たせる文字x,y の値の組は無数にあり,エになる。 (2) りんごとオレンジの個数と,代金について式をつくる




國中數學總複習 6 二元一次聯立方程式 莫博士 帶你長知識 大师链



二元一次聯立方程式 應用題 各校考題 結構數學 國中 發現學習的美麗新世界
國一數學 (下) ─ 二元一次方程式 所謂的未知數,在數學當中,通常以英文字母或x、y、z來表示。 而,未知數所代表的是『元』。 也就是說,在式子當中有幾個未知數,那麼就是代表有『多少元』。 如:x2 (只有一個未知數x,所以是一元)。 xy (有兩個二元一次方程式的圖形《各校考題》 結構數學《國中》 《國一上》負數、數線與整數的四則運算 11 正負數與數線《課程》 11 正負數與數線《自我測驗》 12 整數的加減《課程》 12 整數的加減《自我測驗》 13 整數的乘除《課程》 13 整數的乘除《自我一元一次方程式應用問題 二元一次方程式 二元一次聯立方程式 一元二次方程式 移項法則 整數四則運算 以符號代表未知數 一元一次方程式應用問題 一元一次方程式 二元一次方程式 二元一次聯立方程式 一元二次方程式 移項法則 整數四則運算 以符號




二元一次方程解法



名師課輔網 二元一次方程式題目
13 二元一次聯立方程式應用問題 例題 1 應用問題 1 2 應用問題 2 3 應用問題 3 × 設計內容 第二章、直角坐標平面與二元一次方程式的圖形 (html)二元一次方程式應用問題 《 (32) 2 宣宣以每小時15公里的速度從家裡走到Ubike站 (微笑單車站),再騎Ubike (微笑單車),以每小時 15公里的速度騎到學校,一共花了26分鐘,從家裡 到Ubike 站 再到學校總路程為2公里,試求Ubike 站到學校有多遠?13 二元一次方程式應用問題 第一章 二元一次聯立方程式 國中數學第二冊 國一下,內容包含免費的基本觀念教學影片,訂閱課程就可下載「13 二元一次方程式應用問題」的章節講義pdf檔和無限觀看所有精選題型解說影片,皆由名師葛倫親自教學。



方程初中名师总结二元一次方程应用题 13种经典习题 都是干货 安安股票网




二元一次方程式應用問題2 Youtube
閱讀 > 5 分鐘 4 ex 二元一次式及其值 0523 閱讀 > 11 分鐘 5 ex 化簡二元一次式 1105 閱讀 > 14 分鐘 6 ex 二元一次方程式及其解 14212 X>2,則3X1的範圍為何? 3 若 2X11,則Xa的範圍為何?数学22章連立二元一次方程式「文字を用いた式」<準備問題①> 組 番 名前 1次の にあてはまる数を求めなさい。 1 3 2次の式を,文字の式の表し方にしたがって書きなさい。 3a=3のとき,次の式の値を求めなさい。 12 (1)5-3a (2) a
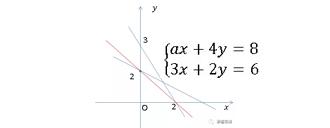



初二数学 图形法秒解含参二元一次方程组问题 知乎




如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl
一 12 解二元一次聯立方程式 1 二元一次聯立方程式 2 代入消去法 3 加減消去法 主題1 二元一次聯立方程式 列二元一次聯立方程式 還記得第 6 頁的情境嗎?已知全票一張 x 元、半票一張 y 元, 小妍買 3 張全票和 1 張半票,共花了 700 元,可列出方程式:3x+y=700; 小翊買 5 張全票和 2 張半票,共花AⅣ4 理解二元一次聯立方程式及其解的意義,並能以代入消去法與加減消去法求解和驗算,以及能運用到日常生活的情境解決問題。 議 題: 閱讀素養教育 核心素養: 系統思考與解決問題 更新時 33 應用問題 國一下 第一章 二元一次聯立方程式 11 二元一次方程式 12 解二元一次方程式 13 二元一次方程式的應用問題 第二章 直角坐標與二元一




均一影片 例題 二元一次方程式 應用問題3 學習單 Shareclass




二元一次聯立方程式的應用題6 Youtube
具體心像,以利「二元一次聯立方程式求解」之學習。 (二)活動適於「二元一次方程式」正式課程之前。 (三)適用年級:(國中七年級以上)。 二、活動目標與核心概念: (一)給定紅色5張、黑色5張牌,任意排成兩列,解決「兩列中紅色牌和黑色牌的 張數差」問題。




复杂的二元一次方程计算题 二元一次方程组计算题 要复杂点的 越复杂越好 5道 三人行教育网 Www 3rxing Org



1 4 聯立方程式 題型解析on Vimeo




解二元一次方程组的方法有哪些 星火网校




七年级数学 二元一次方程组应用题练习及答案详解考前必看 每日头条



名師課輔網 二元一次 工程問題




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



初中数学 求二元一次方程组的参数 哔哩哔哩 つロ干杯 Bilibili



二元一次方程 信息阅读欣赏 信息村 K0w0m Com




二元一次聯立方程式應用問題例4 5 Youtube




像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二



七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客




C 求二元一次方程解 Luojie1011的博客 Csdn博客
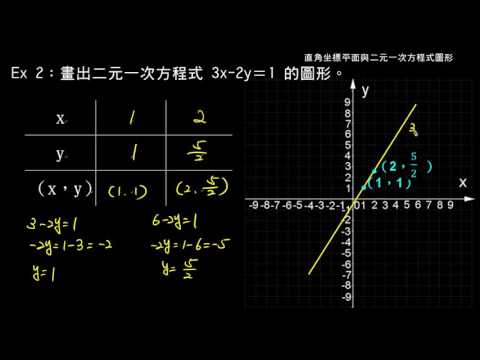



例題 畫出二元一次方程式的圖形 數學 均一教育平台




二元一次方程组应用题练习 Doc 文档分享网




利用numpy模块求解二元一次或多元一次方程 Chengxuxiao的博客 Csdn博客




初中数学 二元一次方程组经典试题解题步骤 含答案 必须收藏




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア
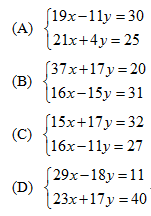



7 X 1 Y 1 為下列哪一個二元一次聯立方程式的解 阿摩線上測驗




二元一次式的化簡綜合應用 Youtube



二元一次方程 信息阅读欣赏 信息村 K0w0m Com




二元一次方程极值二元一次方程既有极小值又有极大值是什么意思




二元一次方程式及其解的意義 Geogebra




二元一次方程式的圖形畫法 Live 多媒體數學觀念典online
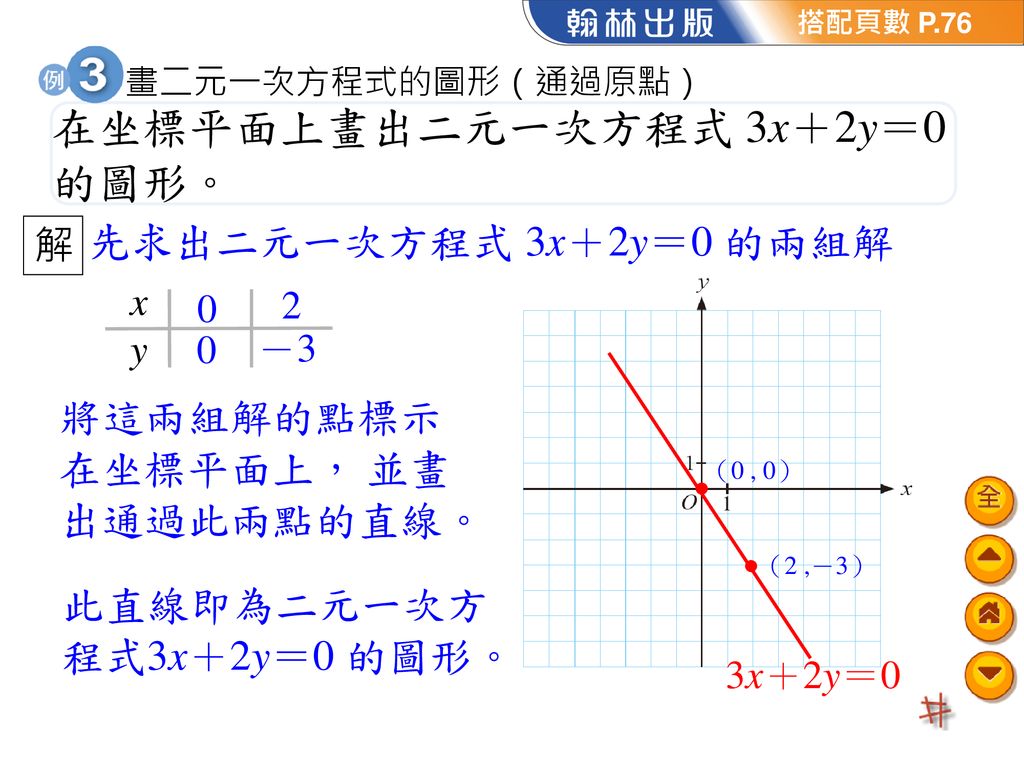



二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download



測評網 國一下 數學第一次段考 複習錦囊



四年级奥数方程问题 三元一次方程组 四年级奥数题 奥数网




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




Java解四元一次方程 台部落



1




Ex 二元一次方程組及其解 Camdemy



如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl



1



二元一次方程解题时常见思路或方法 掌握后基本都是送分的题目 哔哩哔哩 つロ干杯 Bilibili



二元一次聯立方程式解法 二元一次聯立方程式解法線上資訊以及二元一次方程式數學題目認知二元一次聯立方程式題庫 共77筆1 2頁 App開箱王



二元一次方程组练习题100道 松鼠文库




基礎 二元一次聯立方程式 數學 均一教育平台
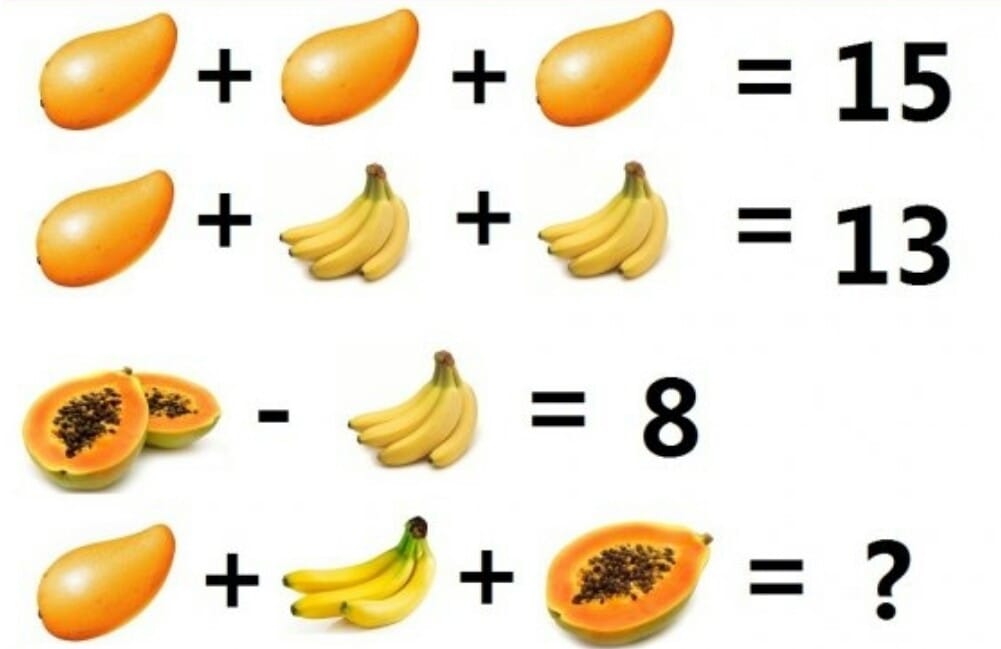



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




第七題 Clear




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org




二元一次聯立方程式的應用題4 數學 均一教育平台




二元一次聯立方程式的應用題3 Youtube




4d F736f F Db2cb3e6a4b8a454a4b8a440a6b8c170a5dfa4e8b57bb2d52e646f63 Pdf 免费下载




二元一次方程组练习题不会 来看看二元一次方程组知识点




連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org




二元一次聯立方程式的基礎概念 數學 均一教育平台




二元一次聯立方程式應用問題例7 Youtube




一元二次方程練習pdf 1 Jkveno




初中数学 二元一次方程 特别需要注意的问题 考生最好看看 每日头条




判斷二元一次方程式及幾組解 數學 均一教育平台




最も欲しかった 数学2 次方程式 ニスヌーピー壁紙




复习专题 解析二元一次方程知识点及应用 知乎




二元一次聯立方程式應用問題 例1 2 3 Youtube




Scratch数学应用篇 解二元一次方程 少儿编程教程网




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




如何用图示展示一个二元一次方程




12 一次方程組與行列式 乙




隨筆誌 二上4 3應用問題 二元一次方程式x Y 比值問題



1 二元一次方程组的矩阵形式 人教版高中选修4 2数学电子课本 数九网




二元一次方程式應用問題1 Youtube




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear



二元一次方程组练习题100道 松鼠文库
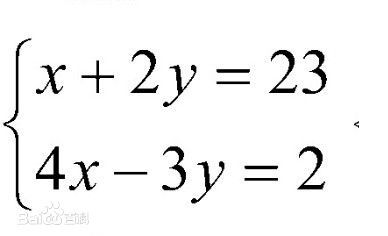



如何用matlab解二元一次方程 百度经验



二元一次聯立方程式 阿摩線上測驗




二元一次方程組應用題 感覺很難好無頭緒 每日頭條




如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl




请问怎么用mathcad解二元一次方程组 雨露学习互助




二元一次方程式的解與圖形 Live 多媒體數學觀念典online




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



二元一次方程组的8个类型 专治各种不会做的应用题
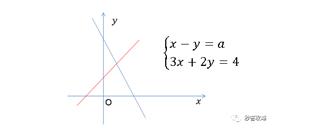



初二数学 函数的思维秒解二元一次方程组问题 看一眼就知道答案 千万别去算 知乎



代入法解二元一次方程组练习题 松鼠文库




二元一次方程组练习题不会 来看看二元一次方程组知识点



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau



1




14初三数学5月二元一次方程组经典题




二元一次复数方程解法 求二元一次方程求解的问题 答案是复数 我想问怎么求得复数的 自己不懂 三人行教育网 Www 3rxing Org




二元一次方程組練習題不會 來看看二元一次方程組知識點 每日頭條




二元一次聯立方程式的幾何意義 Live 多媒體數學觀念典online




如何用图示展示一个二元一次方程




二元一次方程式師父與徒弟的年齡



Http Paperupload Nttu Edu Tw Ca4bd71dbc8ab41 a2e4acc67f2 Pdf




求高手我這三題真的無法這是二元一次聯立方程式應用覺得難 Clear
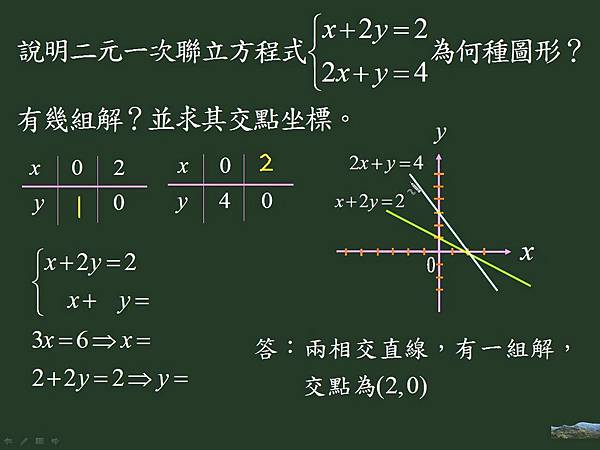



國一下2 2 二元一次方程式的圖形教學資源影片檔案 邦導的天空部落 痞客邦



二元一次方程各类应用题 松鼠文库



0 件のコメント:
コメントを投稿